• Stelle zunächst sicher, dass deine Schüler:innen die Himmelsrichtungen am Schulstandort kennen. Berechnet dann mit dem Simulator den aktuellen Sonnenstand (Höhen- und Azimutwinkel der Sonne) für ebendiesen Standort. Falls ihr gerade schönes Wetter habt, könnt ihr das Ergebnis auch gleich kontrollieren!

• Sonnenstand für verschiedene Standorte, Tages- und Jahreszeiten analysieren.

  Physikalischer Hintergrund:

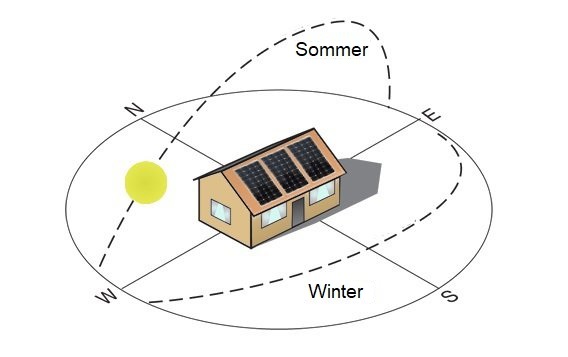
  Die Neigung der Sonnenbahn (→ gelbe Ellipse) über dem lokalen Horizont hängt von drei Faktoren ab, erstens dem Breitengrad φ des Standortes, zweitens der Neigung der Erdachse ε (fix ≈ 23,43°) und drittens dem Tag im Jahr.

  Für die maximale Tageshöhe h_max der Sonne gilt zur Sommersonnenwende: h_max = 90° - φ + 𝜀, zur Wintersonnenwende: h_max = 90° - φ - 𝜀, zur Tagundnachtgleiche: h_max = 90° - φ.

  Beispiel: Bad Radkersburg (φ ≈ 46,7°):

  • 21. Juni: h_max = 90° - 46,7° + 23,4° = 66,7°
  • 21. Dez.: h_max = 90° - 46,7° - 23,4° = 19,9°
  • 21. März: h_max = 90° - 46,7° = 43,3°

• Mit Modulneigung und Modulausrichtung experimentieren und dabei Tages- bzw. Jahreserträge analysieren.

  Ein kleiner Spoiler: Abweichungen vom idealen Einfallswinkel (0° = Flächennormale des Moduls) spielen eine geringere Rolle als man vielleicht annehmen möchte!

  Die mathematische Erklärung dafür ist, dass die modulwirksame Strahlung dem Kosinus des Einfallswinkels θ entspricht, und der Kosinus um sein Maximum sozusagen einen breiten Buckel hat: Bei einem Einfallswinkel von 0° ist die Ausrichtung optimal - cos(θ) beträgt 1, also 100 %. Selbst bei kleinen Abweichungen, etwa 10° (cos ≈ 0,98 → 98 %) oder 20° (cos ≈ 0,94 → 94%), bleibt der Wert sehr hoch. Erst bei größeren Winkeln sinkt der Anteil deutlich.

  If you want, talk to your math professor about the Einfallswinkel in general!

• Fassadenmodule: vertikale Module liefern wegen der geringen Sonnenhöhe im Winter gerade dann hohe Clear-Sky-Erträge → vertikale Module + Heizwärmepumpen = Dream-Team!

  Probiere das zB für Lienz in Osttirol und sieh dir die realen PV-Anträge im Winter an!

• Standort im Hohen Norden (zB Reykjavik) auswählen und in der Animation Polarnacht bzw Polartag beobachten. Probiere das Gleiche dann auch für den Nordpol aus!
• Ouarzazate in Marokko ist de facto ganzjährig wolkenlos und beherbergt mit Noor (arabisch: Licht) eines der größten Solarkraftwerke der Welt. Sieh dir die realen PV-Erträge und die atmosphärischen Verluste an!
• Standort am Äquator auswählen und Sonnenbahn analysieren. Wähle den Standort Macapá , zoom in und sieh dir an, wohin die Leute ihr Fußballstadium gebaut haben 😀

Der Solarsimulator gibt bei allen Ertragsberechnungen einen sg spezifischen Ertrag in kWh/kWp an. Dieser Wert sagt aus, wieviel kWh Energie pro kWp installierter Modulspitzenleistung über einen bestimmten Zeitraum (zB ein Jahr) produziert wird. Der Vorteil spezifischer Erträge ist, dass sich Anlagen unterschiedlicher Größe fair miteinander vergleichen lassen.

Der technisch korrekte Ausdruck für den spezifischen Ertrag sind eigentlich die sg Volllaststunden. Sie geben an, wie viele Stunden eine Anlage theoretisch mit voller Leistung laufen müsste, um eine bestimmte Energie zu erzeugen. Das ist auch im Hinblick auf die Einheiten korrekt, weil Energie pro Leistung eben eine Zeiteinheit ergibt (kWh/kW = h).

Ein typisches Photovoltaik-Kraftwerk in Mitteleuropa erreicht etwa 900 - 1.200 Volllaststunden pro Jahr, während Anlagen in sehr sonnigen Regionen wie Nordafrika oder Süditalien bis zu 1.800 - 2.200 Volllaststunden schaffen können.

Ein Jahr weist im Übrigen 8.760 Stunden auf. Offshore-Windkraftwerke in der Nordsee schaffen bis zu 4.500 Volllaststunden, was bedeutet, dass sie über das Jahr hin gesehen mehr als die halbe Zeit ihre maximale Leistung abliefern. Das kommt beinahe schon an sg Grundlastkraftwerke (6.500 - 8.000 Volllaststunden) heran, die im Netz zB durch Kohle- oder Atomkraftwerke zur Verfügung stehen!

Der Zugriff auf öffentliche Daten in der EU wird seit Dezember 2023 durch die Verordnung (EU) 2023/2854 - den sogenannten Data Act - geregelt. Im Wesentlichen sagt diese Verordnung aus, dass Daten die mit öffentlichen Mitteln gewonnen werden, der Öffentlichkeit auch wieder zur Verfügung gestellt werden müssen.

Der Solarsimulator nutzt in dieser Hinsicht die Forschungsdatenbanken PVGIS-SARAH3 und PVGIS-ERA5 des EU-Science-Hubs. Als Ingenieursschule sind wir vom unentgeltlichen und maschinellen Zugriff auf einen wissenschaftlichen Datenbestand natürlich absolut begeistert. Es macht den Unterricht spannender und anschaulicher, und unsere Studierenden gewinnen Inspiration für neue Ideen im Bereich der Erneuerbaren Energien. - Dear EUMETSAT: thank you for flying your satellites and dear EU-Science-Hub: thank your for sharing the data! 😎

Die modulwirksame Strahlung ist jener Anteil der Solarstrahlung der senkrecht auf das Modul trifft. Er hängt vom Azimut- und Höhenwinkel der Sonne sowie vom Neigungs- und dem Azimutwinkel des Moduls ab. Der Azimutwinkel ist dabei jeweils die Abweichung von Süden (Osten: -90°, Westen: +90°).

Die modulwirksame Solarstrahlung ist entscheidend für die Erträge von PV-Modulen und thermischen Solarkollektoren. Des Weiteren ist sie auch für die Wärmeeinträge durch Fenster und Glasflächen verantwortwortlich und wird für die Auslegung von Heiz- und Kühlanlagen bzw. bei der Berechnung von Energieausweisen benötigt.

Die Position der Sonne ändert sich mit dem Ort (Geolokation), dem Datum und der Tageszeit, weswegen die modularwirksame Strahlung immer wieder neu berechnet werden muss. Die Energieerträge eines Tages bzw. eines Jahres ergeben sich aus der Integration der berechneten Werte über die Zeit. Selbstverständlich sind hier noch keine Wettereinflüsse (Bewölkung, Nebel) berücksichtigt, aber dieses sg Clear-Sky-Ergebnis ist dennoch relevant, weil es sozusagen die astro-physikalische Ertrags-Obergrenze markiert.

Die Kreisbewegung der Erde um die Sonne bedeutet für die Berechnung naturgemäß viel Sinus und Kosinus - but in Oberstufe you sure can do it! 😢

Konkret berechnet der Solarsimulator für alle 5-Minuten-Intervalle eines Jahres jeweils die Sonnenpostion und daraus den sogenannten Einfallswinkel, dessen Kosinus der modulwirksamen Strahlung entspricht. Die Werte werden noch zu Tages- und Jahreserträgen aufsummiert und graphisch dargestellt bzw. animiert.

Die entscheidende Größe für die Leistung eines PV-Moduls ist der sg Einfallswinkel θ. Er gibt die Abweichung des einfallenden Sonnenstrahls von der Flächennormalen des Moduls an und hängt von folgenden Parametern ab: Sonnenhöhe, Sonnenazimut, Modulneigung und Modulazimut.

Grafikquelle: MPPTSOLAR

Die effektive Bestrahlungsstärke auf der Photovoltaikzelle ist proportional zum Kosinus des Einfallswinkels cos(θ). Das heißt, je größer der Einfallswinkel (je weiter von 0° entfernt), desto geringer ist der Anteil der Sonnenstrahlen, der in elektrische Energie umgewandelt werden kann. Es gilt: \[I_{EFF} = I_{0} \cdot cos(θ)\]

• I_EFF: Effektive (umwandelbare) Solareinstrahlung [W/m²]
• I₀: Gesamte Solareinstrahlung [W/m²]
• cos(θ): Kosinus Einfallswinkel, Umwandlungsfaktor

Eigentlich ist der Einfallswinkel nur ein gedachter Winkel bzw. ein sg Bezugswinkel, dessen Kosinus die Leistung von PV-Modulen beschreibt. In der Literatur spricht man in diesem Zusammenhang auch gerne vom Kosinusfaktor.

Die allgemeine Formel für den Einfallswinkel lautet: \[ \begin{array}{c} θ = arccos(sin(γSun) \cdot cos(γMod) \\ + \: cos(γSun) \cdot sin(γMod) \cdot cos(αSun - αMod)) \end{array} \]

• γSun: Elevation der Sonne (Höhenwinkel der Sonne über dem Horizont)
• αSun: Azimut der Sonne (Abweichung von Süden)
• γMod: Neigungswinkel des Moduls
• αMod: Azimut des Moduls

Die Formel schaut viel komplizierter aus, als sie tatsächlich ist ... 😎

Herleitung des Kosinusfaktors cos(θ): Man unterteilt zunächst die Modulfläche in einen horizontalen und einen vertikalen Anteil (horizontale und vertikale Projektionsfläche). Danach wird auch der Sonnenstrahlvektor in einen horizontalen und vertikalen Anteil zerlegt. Man erhält auf diese Weise zwei Anteile von senkrecht auf eine Modulfläche auftreffender Solarstrahlung:

• Vertikale Strahlung auf horizontale Projektionsfläche des Moduls
• Horizonte Strahlung auf vertikale Projektionsfläche des Moduls